在当今的数学领域中，几何学的分支愈发受到重视，半角模型作为一种重要的几何概念，广泛应用于数学、物理及工程学科，本文将深入探讨半角模型专题，帮助读者更好地理解半角模型的原理、应用及其相关知识点。

半角模型概述

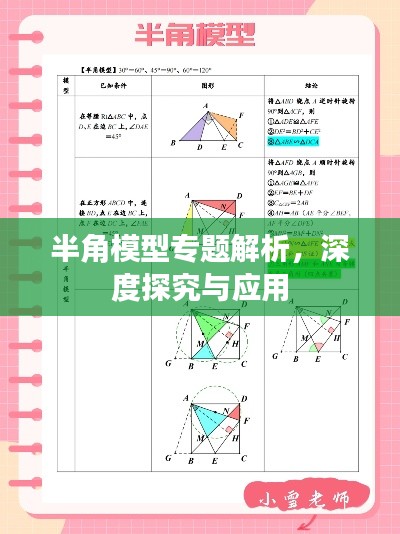
半角模型是几何学中一个关键概念，涉及角度、线段以及三角形等基础知识，半角模型主要探讨的是如何将一个角平分，以及如何通过已知条件求解半角的相关问题，半角模型还涉及到一些高级概念，如相似三角形、三角函数等。

半角模型的原理

半角模型的原理基于角度平分线的性质，在一个角内，通过顶点画出角平分线，将角分为两个相等的部分，半角模型通过这一原理，将复杂的问题简化为求解半角的问题，从而方便求解。

半角模型的应用

半角模型在实际生活中有着广泛的应用，在建筑工程中，半角模型可用于计算建筑物的角度误差；在物理学科中，半角模型可用于求解物体的运动轨迹；在机械制造业中，半角模型可用于设计精密机械零件，半角模型还可以应用于数学竞赛、图形设计等领域。

半角模型专题的解题技巧

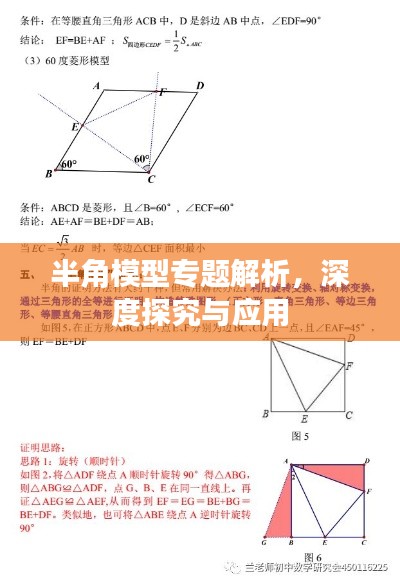
解决半角模型问题，需要掌握一定的解题技巧，要熟练掌握角度平分线的性质，这是解决半角模型问题的关键，要学会将复杂问题简化为半角问题，利用半角模型的原理进行求解，还需要掌握相似三角形、三角函数等知识点，以便更好地解决半角模型问题。

实例分析

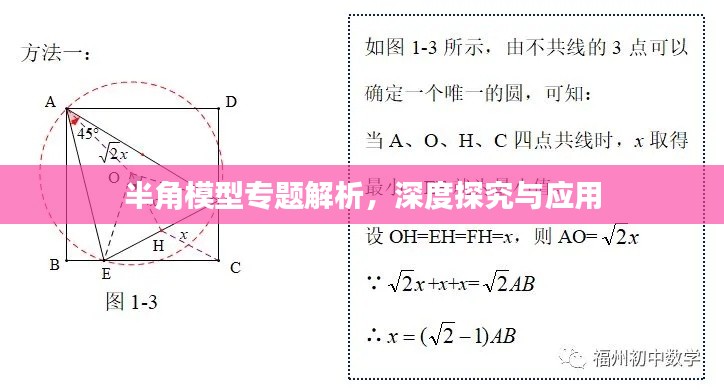
为了更好地理解半角模型，以下是一个实例分析：

假设我们有一个等腰三角形ABC，其中AB=AC，且∠BAC为一个钝角，我们需要求解∠BAC的度数，我们可以通过作AB的垂直平分线DE交AB于点D，交AC于点E，由于DE是AB的垂直平分线，根据半角模型的原理，我们知道∠BAD = ∠CAD = ∠BAC的一半，通过求解∠BAD的度数，我们可以进一步求得∠BAC的度数。

半角模型是几何学中一个重要的概念，掌握半角模型的原理、应用及解题技巧对于提高数学能力具有重要意义，本文详细探讨了半角模型专题，通过实例分析帮助读者更好地理解半角模型的原理和应用，希望读者能够熟练掌握半角模型的相关知识，为今后的学习和工作打下坚实的基础。

建议与展望

为了更好地掌握半角模型专题，建议读者多做练习，熟练掌握角度平分线的性质以及相似三角形、三角函数等知识点，还可以参加数学竞赛、图形设计等活动，通过实践加深对半角模型的理解，展望未来，随着几何学的发展，半角模型的应用将更加广泛，对半角模型的研究也将更加深入。