在数学的立体几何领域中，二面角是一个核心概念，其重要性不言而喻，二面角涉及空间图形的性质、关系以及计算，常常出现在各类几何大题中，本文将围绕二面角的概念、性质、计算方法和实际应用等方面展开讨论，旨在帮助读者深入理解并掌握二面角在立体几何中的应用。

二面角的基本概念

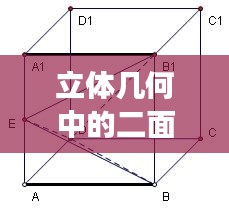
二面角是指两条相交直线所构成的角，其中这两直线分别位于两个不同的平面内，在立体几何中，二面角是描述空间图形的重要手段之一，涉及到图形的旋转、平移、对称等性质，二面角的度数范围通常为0°到180°，表示两个平面的夹角。

二面角的性质

二面角具有一些重要的性质，包括：

1、二面角的度数与两个平面的夹角有关，可以通过计算得到。

2、二面角的性质与图形的旋转、平移和对称等性质密切相关。

3、二面角的大小可以影响图形的体积和其他相关性质。

二面角的计算方法

计算二面角的方法主要包括：

1、通过已知角度计算：如果已知两个平面的夹角，可以通过计算得到二面角的度数。

2、通过已知线段长度计算：在某些情况下，可以通过已知线段长度来计算二面角的度数。

3、通过空间几何图形的性质计算：利用图形的旋转、平移和对称等性质，可以计算二面角的度数。

二面角的实际应用

二面角在立体几何中具有广泛的应用，涉及到建筑、机械、计算机图形学等领域，在建筑设计中，需要考虑建筑物的空间结构和角度，其中就涉及到二面角的应用，在机械工程中，需要考虑机械零件的空间位置和角度，这也需要利用二面角的知识，在计算机图形学中，二面角是描述三维图形的重要手段之一。

立体几何大题中的二面角专题

在立体几何大题中，二面角常常是重要考点，这类题目通常涉及空间图形的性质、关系以及计算，需要考生具备扎实的数学基础和空间想象力，在解决这类问题时，需要灵活运用二面角的性质、计算方法和相关定理，通过逻辑推理和计算得出正确答案。

本文围绕二面角的概念、性质、计算方法和实际应用等方面进行了详细讨论，在立体几何大题中，二面角是重要考点之一，需要考生深入理解和掌握，通过本文的学习，读者应该对二面角有更深入的理解，并能够灵活运用相关知识解决立体几何问题。